
Have them cut out several quadrilaterals of different shapes to check their predictions.

Tear off the corners and place them about the point to confirm that a half turn (or 180°) is created. What do you think will happen?" Students may have encountered this before but let them guess what they think will happen. Say, "I am going to tear off the corners of this triangle and place them around this point (draw point on board). Mark the vertices (corners) of the triangle with different colours. Show the students a large cut out equilateral triangle.Mosaic tiles can be created from fired clay, or cobblestones created from concrete. Tessellation might fit well with efforts to beautify the school environment. Students might be fascinated by the work of Dutch artist Escher, who built his work on distorting regular polygons to create ‘life-like’ tessellation patterns. For example, tessellations are prominent in Islamic art traditions, and in tapa cloth designs from Pacific nations. The contexts for this unit can be adapted to suit the interests and cultural backgrounds of your students. Motivate students to add a new, undiscovered tessellation to the class display. displaying the work of students as models for others, especially students who provide explanations about why particular tessellations work.Then open the investigation to more complex regular polygons triangles, squares, pentagons and hexagons, until generalisations about angles around a vertex emerge. restricting the set of shapes at first, e.g.allow access to calculators and digital tools, so the investigations are more about spatial reasoning than calculation.The difficulty of tasks can be varied in many ways including: Share ideas with the whole class regularly.

Encourage students to work collaboratively in partnerships, and to share and justify their ideas.Make the table accessible to students so they can make predictions about sets of shapes that will, and will not, tessellate. Organise the data about regular polygons in a table, especially the measures of internal angles.Directly model examples of tessellations, and your reasoning about why the combinations of shapes around each vertex will work.Will regular hexagons tessellate? How do you know?, and ask students to justify why they believe patterns occur. Provide physical manipulatives, regular polygons, or virtual equivalents, so that student can experiments with shapes.Here are some approaches to enabling participation. The geometric focus opens up opportunities for visual reasoning that might prove engaging for students who find numeric reasoning challenging. This unit is set for students to learn, and practise, outcomes at Level 4 of mathematics in the New Zealand Curriculum.
POLYGONAL TESSELLATION HOW TO
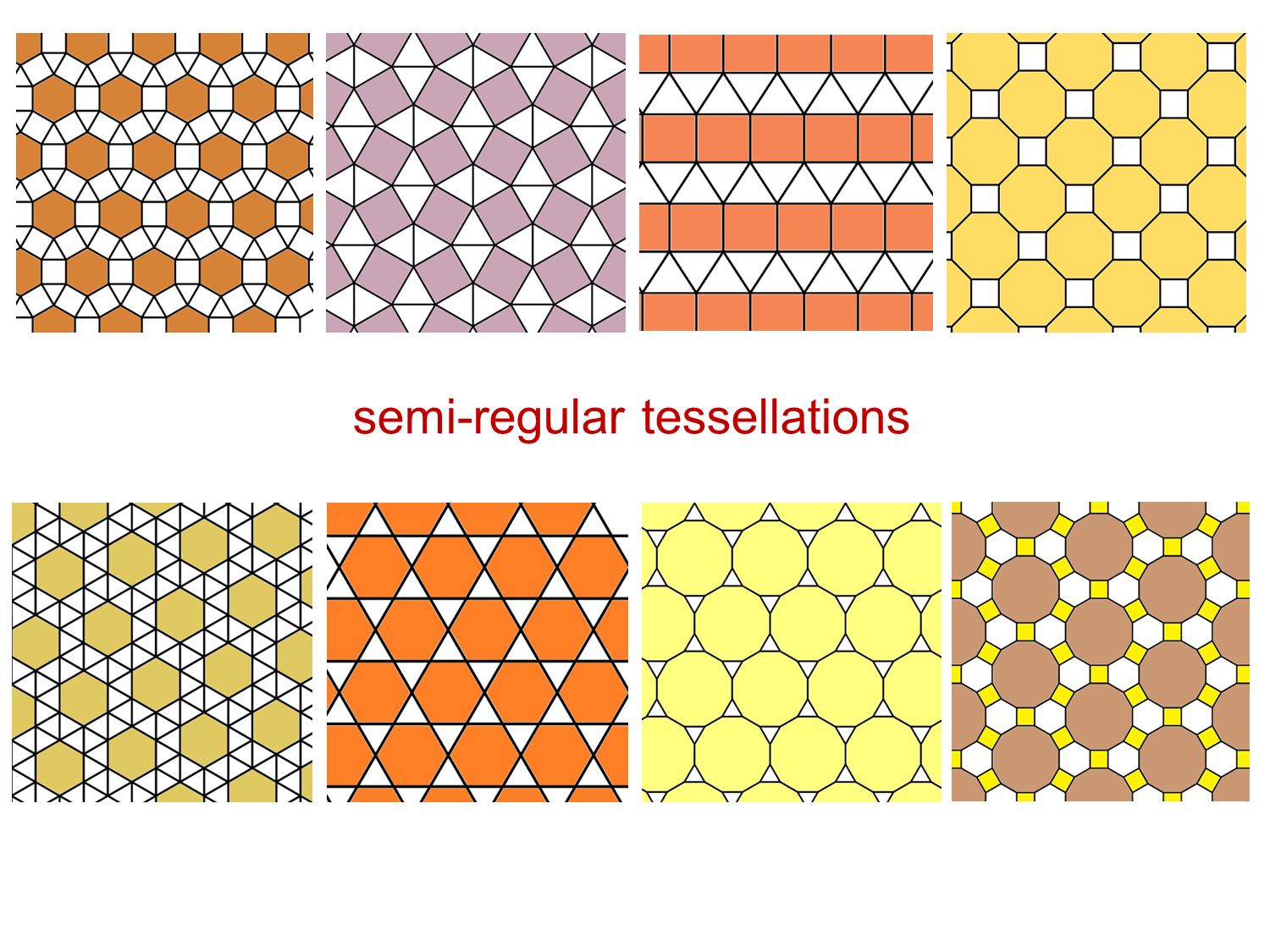
All that they need to know here is how to sum the interior angles of various regular polygons to 360°. Moving on from here, the children can consider semi-regular tilings. This unit thus follows on from Keeping in Shape from Level 3, where regular tessellations are first discussed. This unit takes children through the steps that they need in order to establish that there are only three regular polygons that tile the plane. All of the facts that you need to know are accessible to Level 4 students. To be able to fully understand tessellations using regular polygons, you need to know about their symmetry and about the size of their interior angles. They also provide a nice application of some of the basic properties of polygons. Tessellations are a neat and symmetric form of decoration. You can see them in the pattern on carpets and decorative patterns on containers and packaging. Tessellations are frequently found in kitchen and bathroom tiles and lino.


 0 kommentar(er)
0 kommentar(er)
